反三角函数的复合函数
前言
已知一个函数$ f(x) $,其反函数为$ g(x) $,则$ f(g(x)) = x $。
这本没有问题,但是当你碰到反三角函数的时候,你会发现一个问题。
这是$ f(x) = arcsin(sinx) $的图像:
图像.png)
$ arcsin(sinx) $ 居然不等于 $ x $ !
难道数学老师讲的有问题?
答案当然是否定的
关于反三角函数
其实问题的关键是对于反三角函数的理解,以下以$ arcsinx $为例。
当我们尝试取$ sinx $的反函数的时候你会发现,$ sinx $本身是没有反函数的。因为一个函数有反函数的充要条件是这个函数是一一映射的。换句话说,这个函数的$ y $对应且仅对应一个$ x $。但是我们知道,三角函数都是周期函数,它必定不会是一一对应的。
但有时候,我们需要根据数值求角度。而三角函数的周期性就很好的解决了这个问题,既然我们只需要知道一个角度,其他可以进行推算,那么只需要截取一个周期下来就可以了。
所以,我们现在的$ arcsinx $就诞生了,而那个被截下来的那部分称为主值区间。
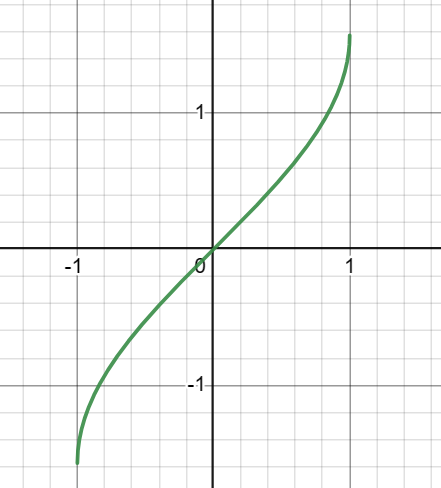
如$ f(x) = arcsinx $:
结论
所以,从根本上说,$ arcsinx $其实不是$ sinx $的反函数。但是如果我们令$f(x) = sinx ,x \in [-\frac{\pi}{2},\frac{\pi}{2}]$, $ g(x) = arcsinx $,那么$ f(x) $ 和 $ g(x) $就互为反函数。
注意
这个结论有什么用呢?其实,最主要的是要提醒自己反三角函数和其他反函数的不一样之处。不能随意套用结论,很容易就犯下这个错误。