异构和泰勒展开
前言
说实话,我不是很确定大学考试需不需要用到这一部分的知识,因为证明不等式已经不像是高中一样只有只用手段:求导。不过从目前来看,在第三章中还是有用武之地的,至少从我我看到的题目来看是有用的。
异构
什么是异构?异构就是构造相异的函数。异构对于不等式只有一种玩法:保值性。保值性其实我们初中就学过,假如$a\geq0$ 那么$a+|b|+\sqrt{c^2}$一定是大于等于$0$的。这里我就不多做解释了
泰勒展开
这个大家最近都学过,我也不过多阐释,仅在这里写几个常用的麦克劳林公式:
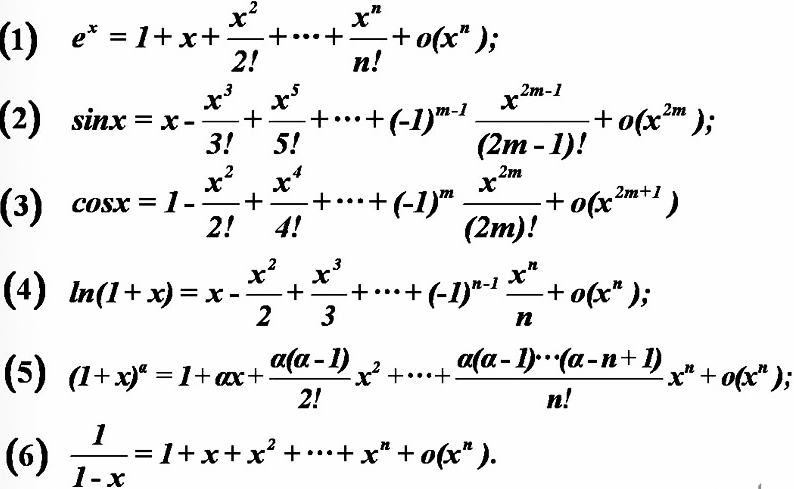
异构与泰勒展开
这里,才是本文最重要的核心。 刚刚我们提到异构是构建相异的函数,那么这个函数怎么来呢? 我们先分析一下,假设我们要证明一个不等式$f(x)>g(x)$,那么根据异构的思路,我们就要从原始式子构造成这样$ p(x)+q(x)>0 $其中$p(x)\geq0,q(x)\geq0$。如果说原式要取等号,那么还需要满足$p(x)$和$q(x)$同时在某处取等。 这个时候泰勒展开闪亮登场,理由我们慢慢说来: 我们先看看带有拉格朗日余项的$n$阶泰勒公式:
$f(x)=f(x_0)+f’(x_0)(x-x_0)+\frac{f^{‘’}(x_0)}{2!}(x-x_0)^2+\ldots+\frac{f^n(x_0)}{n!}+R_n(x)$
其中
$R_n(x)=\frac{f^{(n+1)} (\xi)}{(n+1)!}(x-x_0)^{(n+1)}$这里$\xi$是$x_0$与$x$站之间的某个值。
观察上述式子,左边后右边关键相等的是哪一个东西?
对,就是余项$R_n(x)$,这个东西其实就是一个逼近拟合的误差。所以,当我们去掉这个误差的时候,这就是一个不等式了。
接下来问题来了,那么它到底是大于还是小于呢?
其实还是看余项,这也是为什么我们看到是带有拉格朗日余项的泰勒展开,因为它好判断正负呀。如果它是正的,那么左边大于右边,如果它是负的,那么右边大于左边。
所以,我们只需要把余项取掉,把右边丢过来,就可以获得一个关于此函数的不等式。
好,大于小于解决了,那么取等呢?
我们们试试把$x_0$带入原式看看,欸,你会发现,左右两边相等!
这也就意味着,$x_0$就是它的一个零点。它的取等条件也是这个。
因此,泰勒展开基本完美的解决了这类非初等函数的寻找不等式的问题。
接下来,我将以作业本上的题为例,讲述一下如何操作:
证明下列不等式: $-e^{-x} + sinx < 1 + \frac{x^2}{2} (0 < x < 1)$
法一(端点效应):
解析:略
令$f(x)=e^{-x} - \frac{x^2}{2} + sinx -1$
$f’(x)=-e^{-x} -x + cosx $
$f^{‘’}(f) = e^{-x} - 1 - sinx < 0, f(x)$在$(0,1)$上单调递减
又$f(0) = 0$
所以$f(x) < f(0) = 0$
即$f(x) < 0$
法二(异构):
解析: 异构强调的是观察能力。 在此处有$e^x$,有$\frac{1}{2}x^2$还有$sinx$。 不难猜想出$e^x$的二阶展开和$sinx$的一阶展开。
$ e^{-x} + sinx < 1 + \frac{x^2}{2} $
$ \Longrightarrow e^{-x} - \frac{1}{2}x^2 + x - 1 < x - sinx $
因为$ e^x = 1 + x + \frac{1}{2}x^2 + \frac{e^{\xi_1}}{6}x^3 $
所以当$ x < 0 $时,$e^x < 1 + x + \frac{1}{2}x^2$
所以当$ x \in (0 , 1) $时,$e^{-x} < 1 - x + \frac{1}{2}x^2 \Longrightarrow e^{-x} - \frac{1}{2}x^2 + x - 1 < 0$
因为 $ sinx = x - \frac{cos\xi_2}{6}x^3$
所以当$ x \in (0 , 1) $时,$ sinx < x \Longrightarrow x - sinx > 0 $
所以$ x - sinx > 0 > e^x - \frac{1}{2}x^2 + x - 1 $
即$ e^{-x} - \frac{1}{2}x^2 + x - 1 < x - sinx$
原不等式得证。
结语
异构这个方法,它本质是将很难求导处理的问题简单化,所以,这种方法不是在所有地方都非常方便。就像这道列题,你会发现,你用端点效应要写的少的多,当然,异构给你的计算量就少一点,因为你只要观察出了$e^x$的二阶展开,和$sinx$的一阶展开就很好做了。 总之,方法毕竟是方法,它是给我们用的,我们不能被方法所绑架,在合适的时候选取合适的方法才是必胜之道。